PROCESO DE DESARROLLO DE PERALTES EN DISEÑO GEOMÉTRICO DE CARRETERAS – AUTO EVALUACIÓN DE ACTIVIDADES
Para el proceso de diseño y cálculo de desarrollo de peraltes en curvas horizontales, se lo realizará en base a los siguientes esquemas

La transición del peralte deberá llevarse a cabo combinando las tres condiciones siguientes:
- Características dinámicas aceptables para el vehículo.
- Rápida evacuación de las aguas de la calzada.
- Sensación, estética agradable.
La variación del peralte requiere una longitud mínima, de forma que no se supere un determinado valor máximo de la inclinación que cualquier borde de la calzada tenga con relación a la del eje de giro del peralte.
Eje de Rotación: Es el cambio de la sección transversal de bombeo a peralte, es decir, es el cambio de inclinación transversal de la calzada.
Para elegir el eje de rotación consideramos cinco factores:
Ø Cuestiones relativas al drenaje
Ø Diferencia admisible de cota entre los bordes extremos de la calzada.
Ø Adaptación de la sección transversal al terreno natural.
Ø Consideraciones estéticas, económicas y de seguridad.
Ø Necesidad de resultantes de intersecciones a nivel o de zona de enlace.
¿Cuándo se escoge como eje de rotación el eje de la calzada?
En calzadas simples se recomienda usar como eje de rotación al eje de la calzada y también cuando se produce problemas de drenaje o cuando el pavimento se encuentra en altura mínima sobre cuneta.
¿Cuándo se escoge el borde externo como eje de rotación?
Ø Por razones estéticas.
Ø Cuando el uso del suelo adyacente no resulte conveniente para elevar la cota de borde.
Cuando hay cantero central y no es muy ancho, se recomienda usar como eje de rotación éste, pero si es muy ancho, no.
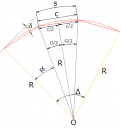
Para el desarrollo de peraltes en curvas circulares simples, se toma el siguiente esquema y fórmulas para elaborar la planilla de variación de inclinaciones transversales de la plataforma, tanto en recta como en curva horizontal.
LC : Longitud de Curva Circular [m]
b : Inclinación Transversal del Bombeo [%]
e : Inclinación Transversal del Peralte [%]
EJEMPLO DE CÁLCULO:
Realizar el Desarrollo de Peralte de la siguiente Curva Circular Simple con los siguientes datos:
LC = 66.954 m
PC = 0+419.498
PT = 0+486.453
e = 8 %
b = 2 %
Giro = Derecho
En base a lo explicado, elaborar el desarrollo de peraltes y resolver el replanteo para la construcción de la sección transversal de carretera.
Lista de cotejo para la auto-evaluación del trabajo del presente módulo
Aspectos a Evaluar
|
si
|
no
|
justificación
|
Organicé mi horario para trabajar el módulo.
|
x
|
Es importante para una buena planificación del módulo
| |
Leí la guía de aprendizaje al inicio del módulo.
|
x
|
Para analizar el contenido necesario para las tareas
| |
Leí las orientaciones de cada actividad.
|
x
|
Para profundizar las tareas específicas
| |
Leí las consignas de las actividades en la plataforma antes de realizarlas.
|
x
|
Para entenderlo simultáneamente al realizar las tareas
| |
Leí los contenidos al inicio del módulo
|
x
|
Para entender el contenido del mismo
| |
Realicé el mapa siguiendo las instrucciones y tomando en cuenta la lista de cotejo.
|
x
|
Para un mejor entendimiento de lo requerido
| |
Leí y respondí los correos del curso.
|
x
|
Para interactuar conceptos específicos
| |
Ingresé frecuentemente al curso durante la unidad.
|
x
|
Para mantenerme informado de las actividades acerca del presente módulo
| |
Comprendí todos los contenidos de la unidad.
|
x
|
Es claro y conciso
| |
Mi desempeño general en esta primera unidad, me permitió alcanzar los objetivos de la unidad.
|
x
|
Son herramientas interesantes que mejorarán el proceso de enseñanza
|
Para una curva circular simple se tienen los siguientes elementos:
- Rumbo de la tangente de entrada: N 76º20′ E.
- Rumbo de la tangente de salida: N 19º40′ E.
- Abscisa del punto de intersección de las tangentes, PI: k2+226.
- Coordenadas del PI: 800 N , 700 E.
- Cuerda unidad: 20 m.
- Radio de curvatura: 150 m.
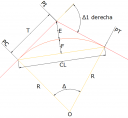
Curvas Circulares Simples
Las curvas circulares simples se definen como arcos de circunferencia de un solo radio que son utilizados para unir dos alineamientos rectos de una vía.
- Ángulo de deflexión [Δ]: El que se forma con la prolongación de uno de los alineamientos rectos y el siguiente. Puede ser a la izquierda o a la derecha según si está medido en sentido anti-horario o a favor de las manecillas del reloj, respectivamente. Es igual al ángulo central subtendido por el arco (Δ).
- Tangente [T]: Distancia desde el punto de intersección de las tangentes (PI) -los alineamientos rectos también se conocen con el nombre de tangentes, si se trata del tramo recto que queda entre dos curvas se le llama entretangencia– hasta cualquiera de los puntos de tangencia de la curva (PC o PT).
- Radio [R]: El de la circunferencia que describe el arco de la curva.
- Cuerda larga [CL]: Línea recta que une al punto de tangencia donde comienza la curva (PC) y al punto de tangencia donde termina (PT).
- Externa [E]: Distancia desde el PI al punto medio de la curva sobre el arco.
- Ordenada Media [M] (o flecha [F]): Distancia desde el punto medio de la curva hasta el punto medio de la cuerda larga.
- Grado de curvatura [G]: Corresponde al ángulo central subtendido por un arco o una cuerda unidad de determinada longitud, establecida como cuerda unidad (c) o arco unidad (s).
Ver más adelante para mayor información. - Longitud de la curva [L]: Distancia desde el PC hasta el PT recorriendo el arco de la curva, o bien, una poligonal abierta formada por una sucesión de cuerdas rectas de una longitud relativamente corta.
Ver más adelante para mayor información.
Ahora vamos a detenernos en dos aspectos con un poco más de detalle:
Grado de curvatura
Usando arcos unidad: En este caso la curva se asimila como una sucesión de arcos pequeños (de longitud predeterminada), llamados arcos unidad (s). Comparando el arco de una circunferencia completa (2πR), que subtiende un ángulo de 360º, con un arco unidad (s), que subtiende un ángulo Gs (Grado de curvatura) se tiene:
Usando cuerdas unidad:
Este caso es el más común para calcular y materializar (plasmar en el terreno) una curva circular, pues se asume que la curva es una sucesión de tramos rectos de corta longitud (también predeterminada antes de empezar el diseño), llamados cuerda unidad (c). La continuidad de esos tramos rectos se asemeja a la forma del arco de la curva (sin producir un error considerable). Este sistema es mucho más usado porque es más fácil medir en el terreno distancias rectas que distancias curvas
(pregunta: ¿Se pueden medir distancias curvas en el terreno utilizando técnicas de topografía?¿cómo?).
Tomando una cuerda unidad (c), inscrita dentro del arco de la curva se forman dos triángulos rectángulos como se muestra en la figura, de donde:
Longitud de la curva
A partir de la información anterior podemos relacionar longitudes con ángulos centrales, de manera que se tiene:
Usando arcos unidad:
Usando cuerdas unidad:
La longitud de una cuerda unidad, o de un arco unidad, se toma comúnmente como 5 m , 10 m , ó 20 m .
Localización de una curva circular
Para calcular y localizar (materializar) una curva circular a menudo se utilizan ángulos de deflexión.
Un ángulo de deflexión (δ) es el que se forma entre cualquier línea tangente a la curva y la cuerda que va desde el punto de tangencia y cualquier otro punto sobre la curva.
Como se observa en la figura, el ángulo de deflexión (δ) es igual a la mitad del ángulo central subtendido por la cuerda en cuestión (Φ).
Entonces se tiene una deflexión para cada cuerda unidad, dada por:
Es decir, se puede construir una curva con deflexiones sucesivas desde el PC, midiendo cuerdas unidad desde allí. Sin embargo, rara vez las abscisas del PC o del PT son cerradas (múltiplos exactos de la cuerda unidad), por lo que resulta más sencillo calcular una subcuerda desde el PC hasta la siguiente abscisa cerrada y, de igual manera, desde la última abscisa cerrada antes del PT hasta él.
Para tales subcuerdas se puede calcular una deflexión conociendo primero la deflexión correspondiente a una cuerda de un metro (1 m ) de longitud δm:
Entonces la deflexión de las subcuerdas se calcula como:
δsc = δm · Longitud de la subcuerda
La deflexión para el PT, desde el PC, según lo anotado, debe ser igual al la mitad del ángulo de deflexión de la curva:
δPT = Δ/2
Lo cual sirve para comprobar la precisión en los cálculos o de la localización en el terreno.
Ejemplo
Para una curva circular simple se tienen los siguientes elementos:
- Rumbo de la tangente de entrada: N 76º20′ E
- Rumbo de la tangente de salida: N 19º40′ E
- Abscisa del punto de intersección de las tangentes, PI: k2+226
- Coordenadas del PI: 800 N , 700 E
- Cuerda unidad: 20 m
- Radio de curvatura: 150 m
Calcular los elementos geométricos de la curva; las abscisas del PC y el PT; las coordenadas del PC, el PT y el centro de la curva; y las deflexiones de la curva.
Solución
Elementos geométricos de la curva
El ángulo de deflexión de la curva está dado por la diferencia de los rumbos de los alineamientos (no siempre es así, en este caso sí porque los dos están en el mismo cuadrante NE):
Δ = 76º20′ – 19º40′ = 56º40′ Izquierda
(A la izquierda porque el rumbo de la tangente de salida es menor que el de la de entrada)
Conociendo el radio y el ángulo de deflexión se pueden calcular los demás elementos geométricos:
Tangente: T = R · Tan (Δ/2)
Grado de curvatura: Gc = 2 · Sen-1[ c / (2R) ]
Longitud de la curva: Lc = c·Δ/Gc
Cuerda Larga: CL = 2·RSen(Δ/2)
Externa: E = R(1/Cos(Δ/2) – 1)
Ordenada Media (Flecha): M = R[1 – Cos(Δ/2)]
Deflexión por cuerda: 
Deflexión por metro: 
Abscisas del PC y el PT
Conociendo la abscisa del PI y las longitudes, tanto de la tangente (T) como de la curva (Lc):
Abscisa del PC = Abscisa del PI – T
Abscisa del PC = k2 + 226 – 80,879 m = k2 + 145,121
Abscisa del PC = k2 + 226 – 80,879 m = k2 + 145,121
Abscisa del PT = Abscisa del PC + Lc
Abscisa del PT = k2 + 145,121 + 148,243 m = k2 + 293,364
Abscisa del PT = k2 + 145,121 + 148,243 m = k2 + 293,364
Se debe tener en cuenta que la abscisa del PT se calcula a partir de la del PC y NO del PI, pues la curva acorta distancia respecto a los alineamientos rectos.
- Coordenadas de los puntos PC, PT y O
Conociendo los rumbos de las tangentes de entrada y salida se pueden calcular sus azimutes:
Azimut del PC al PI = 76º 20′
Azimut del PI al PC = Contra azimut de PC-PI = 76º 20′ + 180º = 256º 20′
Azimut del PC a O = 256º 20′ + 90º = 346º 20′ (porque el radio es perpendicular a la tangente de entrada en el PC)
Azimut del PI al PT = 19º 40′
Azimut del PI al PC = Contra azimut de PC-PI = 76º 20′ + 180º = 256º 20′
Azimut del PC a O = 256º 20′ + 90º = 346º 20′ (porque el radio es perpendicular a la tangente de entrada en el PC)
Azimut del PI al PT = 19º 40′
Nota: Debe tenerse mucho cuidado con el cálculo de estos azimuts, pues las condiciones particulares de cada curva pueden hacer que cambie la manera de calcularlos. Especialmente el hecho de si el ángulo de deflexión es a la izquierda o a la derecha. Lo que yo recomiendo para no cometer errores es, primero que todo, tener bien claro el concepto de azimut, y luego hacer un dibujo representativo para ubicarse, que sea claro y más o menos a escala.
Recordemos que, conociendo las coordenadas de un punto A (NA y EA), las coordenadas de un punto B (NB y EB) se calculan a partir de la distancia y el azimut de la linea que une los dos puntos (AB) así:
NB = NA + DistanciaAB · Cos(AzimutAB)
EB = EA + DistanciaAB · Sen(AzimutAB)
EB = EA + DistanciaAB · Sen(AzimutAB)
Coordenadas del PI:
800N 700E
Coordenadas del PC:
N = 800 + T·Cos(256º 20′) = 800 + 80,879 Cos(256º 20′)
N = 780,890
E = 700 + T·Sen(256º 20′) = 700 + 80,879 Sen(256º 20′)
E = 621,411
Coordenadas del centro de la curva (O):
N = 780,890 + R·Cos(346º20′) = 780,890 + 150 Cos(346º20′)
N = 926,643
E = 621,411 + R·Sen(346º20′) = 621,411 + 150 Sen(346º20′)
E = 585,970
Coordenadas del PT
N = 800 + T·Cos(19º40′) = 800 + 80,879 Cos(19º40′)
N = 876,161
E = 700 + T·Sen(19º40′) = 700 + 80,879 Sen(19º40′)
E = 727,220
- Deflexiones de la curva
Para calcular las deflexiones de la curva partimos de las abscisas calculadas para el PC y el PT y dos ángulos que ya están definidos: la deflexión por cuerda y la deflexión por metro.
Como la cuerda unidad es de 20 m quiere decir que las abscisas de la poligonal se vienen marcando a esa distancia, por lo tanto si la abscisa del PC es la k2 + 145,121 , la siguiente abscisa cerrada corresponde a la k2 + 160 (no la k2 + 150 porque no es múltiplo de 20, es decir, si empezamos desde la k0 + 000 sumando de 20 en 20 no llegamos a la k2 + 150 sino a la k2 + 160). Esto genera una subcuerda, cuya longitud se calcula como la diferencia entre las dos abscisas:
- Subcuerda de entrada: 2 160 m – 2 145,121 m = 14,879 m
Ahora, si ya se había calculado que por cada metro de curva existe una deflexión δm=0º11’28,06”, para la primera subcuerda tenemos una deflexión (correspondiente a la abscisa k2 + 160) de:
- Deflexión para la abscisa k2 + 160 = 14,879 m * 0º11’28,06” = 2º50’37,64”
A partir de la abscisa k2 + 160 siguen abscisas cerradas cada 20 m (de acuerdo a la longitud de la cuerda unidad), hasta llegar al PC, y la deflexión para cada una de las abscisas siguientes corresponde a la suma de la anterior con la deflexión por cuerda:
- Deflexión para la k2+180 = 2º50’37,64” + 3º49’21,2” = 6º39’58.84”
- Deflexión para la k2+200 = 6º39’58.84” + 3º49’21,2” = 10º29’20,04”
- Deflexión para la k2+220 = 10º29’20,04” + 3º49’21,2” = 14º18’41,24”
- Deflexión para la k2+240 = 14º18’41,24” + 3º49’21,2” = 18º08’02,44”
- Deflexión para la k2+260 = 18º08’02,44” + 3º49’21,2” = 21º57’23,64”
- Deflexión para la k2+280 = 21º57’23,64” + 3º49’21,2” = 25º46’44,84”
Pero ahí hay que parar porque la abscisa del PT es la k2 + 293,364 , por lo tanto se genera otra subcuerda, la de salida, que se calcula de manera similar a la de entrada:
- Subcuerda de salida: 2 293,364 m – 2 280 m = 13,364
Y de la misma manera, la deflexión para la subcuerda es de:
- Deflexión para la subcuerda de salida = 13,364 m * 0º11’28,06” = 2º33’15,23”
Así que al final, la deflexión para el PT es:
- Deflexión para la k2+293,364 = 25º46’44,84” + 2º33’15,23” = 28º20’00,07”
La cual, según lo visto en el artículo, debe corresponder con la mitad del ángulo de deflexión de la curva:
Con esta información se construye la cartera de deflexiones, que va a ser la que permita materializar la curva en el terreno, pues es la que recibe el topógrafo para hacer su trabajo. A continuación se muestran las tres primeras que debe contener dicha cartera. Las otras tres, hacen referencia a los elementos que ya se calcularon a lo largo de este artículo (es necesario reescribirlos dentro de la cartera), el azimut de los alineamientos rectos (de entrada y salida), y el sentido en el que se deflectará la curva (en este ejemplo desde el PC hasta el PT, que es el sentido en el que aumenta la deflexión). Nótese que la cartera está escrita de abajo hacia arriba, para facilitar el trabajo de los topógrafos.
| ESTACIÓN | ABSCISA | DEFLEXIÓN |
| PT | k2+293,364 | 28º20’00,07” |
| K2+280 | 25º46’44,84” | |
| K2+260 | 21º57’23,64” | |
| K2+240 | 18º08’02,44” | |
| K2+220 | 14º18’41,24” | |
| K2+200 | 10º29’20,04” | |
| K2+180 | 6º39’58.84” | |
| K2+160 | 2º50’37,64” | |
| PC | k2+145,121 | 0º00’00” |
Enlace del video: https://www.youtube.com/watch?v=EW8Q6gUcm0A










No hay comentarios:
Publicar un comentario